MEL TECH
CIRCTRONICS
Thevenin's and Norton's Theorem
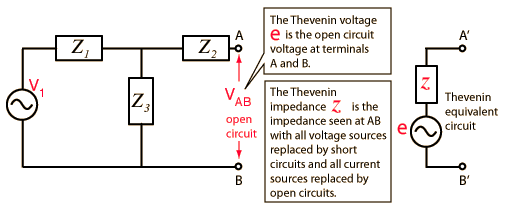
Any combination of sinusoidal AC sources and impedances with two terminals can be replaced by a single voltage source e and a single series impedance z. The value of e is the open circuit voltage at the terminals, and the value of z is e divided by the current with the terminals short circuited. In this case, that impedance evaluation involves a series-parallel combination.
Using Thévenin's Theorem is especially advantageous when:
· we want to concentrate on a specific portion of a circuit. The rest of the circuit can be replaced by a simple Thévenin equivalent.
· we have to study the circuit with different load values at the terminals. Using the Thévenin equivalent we can avoid having to analyze the complex original circuit each time.
We can calculate the Thévenin equivalent circuit in two steps:
1. Calculate ZTh. Set all sources to zero (replace voltage sources by short circuits and current sources by open circuits) and then find the total impedance between the two terminals.
2. Calculate VTh. Find the open circuit voltage between the terminals.
Norton's Theorem, already presented for DC circuits, can also be used in AC circuits. Norton's Theorem applied to AC circuits states that the network can be replaced by a current source in parallel with an impedance.
We can calculate the Norton equivalent circuit in two steps:
1. Calculate ZTh. Set all sources to zero (replace voltage sources by short circuits and current sources by open circuits) and then find the total impedance between the two terminals.
2. Calculate ITh. Find the short circuit current between the terminals.
Now let's see some simple examples.
The first step is to find the open circuit voltage between points A and B:
The open circuit voltage using voltage division:
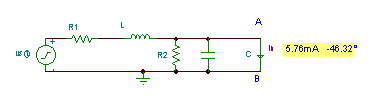
Example 1:
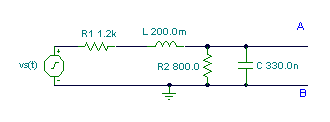
Find the Thévenin equivalent of the network for the points A and B at a frequency: f = 1 kHz, vS(t) = 10 cosw×t V.

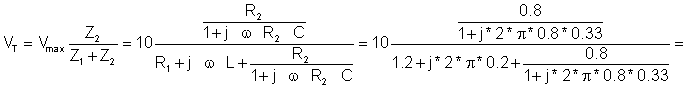
= -0.065 - j2.462 = 2.463 e-j91.5º V
The second step is to replace the voltage source by a short circuit and to find the impedance between points A and B:
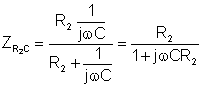
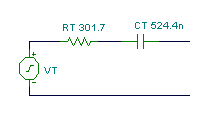
Here is the Thévenin equivalent circuit, valid only at a frequency of 1kHz. We must first, however, solve for CT's capacitance. Using the relationship 1/wCT = 304 ohm, we find CT = 0.524 uF
Now we have the solution: RT = 301 ohm and CT = 0.524 m F:

Example 2:
Find the Norton equivalent of the circuit in Example 1.
f = 1 kHz, vS(t) = 10 cosw×t V.
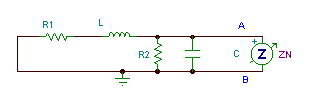
The equivalent impedance is the same:

ZN=(0.301-j0.304) kohm
Next, find the short-circuit current:

IN = (3.97-j4.16) mA
Then the short-circuit current:
And finally the Norton equivalent: