MEL TECH
CIRCTRONICS
BALANCED THREE - PHASE CIRCUIT
The voltages in the three-phase power system are produced by a synchronous generator. In a balanced system, each of the three instantaneous voltages have equal amplitudes but separated from the other voltages by a phase angle of 120 . The three voltages (or phases) are typically labeled a, b and c. The common reference point for the three phase voltages is designated as the neutral connection and is labeled as n. We may define either a positive phase sequence (abc) or a negative phase an bn cn sequence (acb) as shown below. The three sources Van , Vbn and Vcn are designated as the line-to-neutral voltages in the three-phase system.
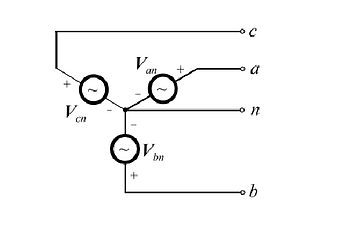

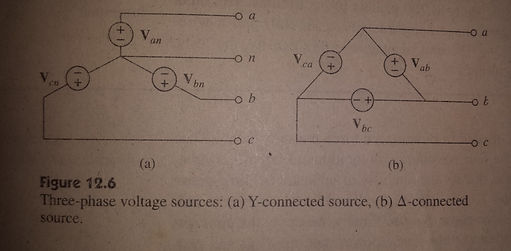
An alternative way of defining the voltages in a balanced three-phase system is to define the voltage differences between the phases. These voltages are designated as line-to-line voltages. The line-to-line voltages can be expressed in terms of the line-to-neutral voltages.
First, the wye - connected voltages Van, Vbn, and Vcn are respectively between lines a, b, c, and the neutral line n. These are called phase voltages. The voltages are said to be balanced phase voltages if the voltages sources have the same amplitude and frequency w and are out of phase by 120degrees.
Van = Vp∠0
Vbn = Vp∠-120
Vcn = Vp∠-240 = Vp∠120
where Vp is the effective or rms value of the phase voltage. this is known as abc sequence or positive sequence, Van leads Vbn, which turn leads Vcn. This rotates counterclockwise. For negative or acb sequence, Van leads Vcn, ehich turn leads Vbn. this rotates clockwise direction.
LINE - TO - LINE VOLTAGES
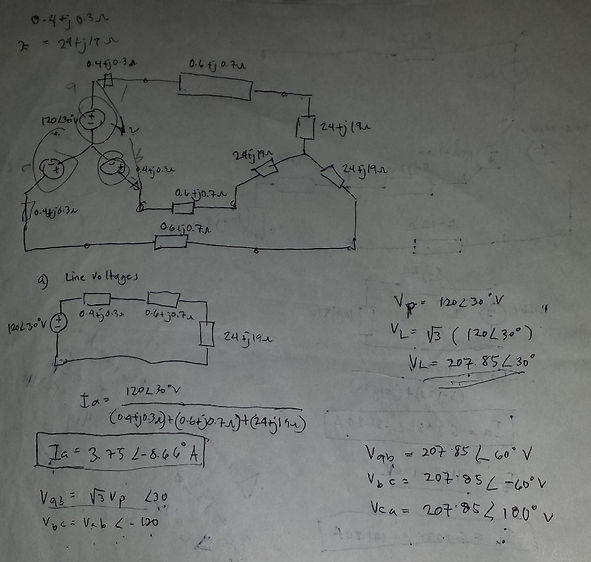
Example:
Van + Vbn + Vcn = Vp∠0 + Vp∠-120 + Vp∠120
= Vp( 1.0 - 0.5 -j0.866 - 0.5+j0.866)
= 0
Three - Phase Connections
The sources and loads in a three-phase system can each be connected in either a wye (Y) or delta (Δ) configuration. Note that the wye connections are line-to-neutral while the delta connections are line-to-line with no neutral.
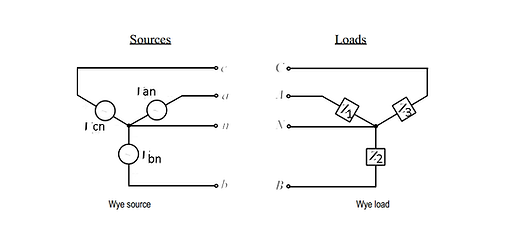
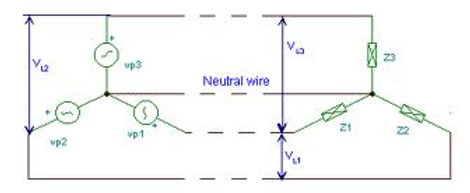
BALANCED WYE - WYE CONNECTION
A balanced Y-Y system is a three-phase system with a balanced y-connected source and a balanced y-connected load.
Example:
1.
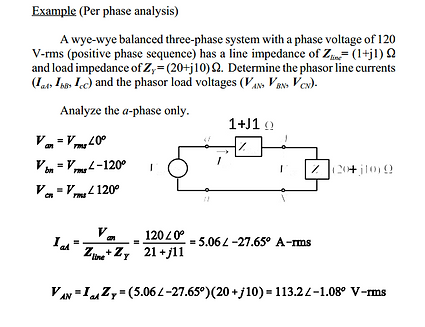

2.
BALANCED WYE - DELTA CONNECTION
A balanced Y-Δ system consists of a balanced y-connected source feeding a balnced Δ-connected load.

The line voltages are: Vab = √3 Vp∠30
Vbc = √3 Vp∠-90
Vca = √3 Vp∠-150
Iab = Vab/ZΔ
Ibc = Vbc/ZΔ
Ica = Vca/ZΔ
Current Load(IL) = √3 Ip
Zy = ZΔ/3
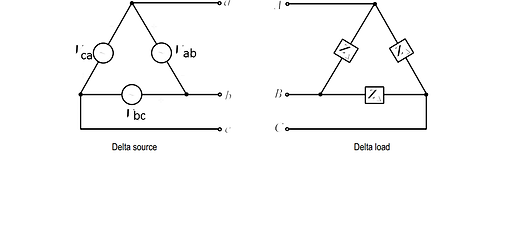
BALANCED DELTA - DELTA CONNECTION
A balanced Δ-Δ system is one which both the balanced source and balanced load are Δ-connected.
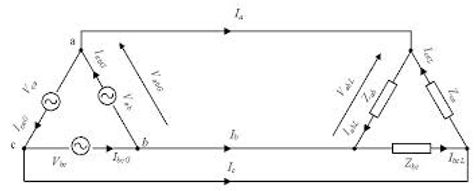
IL= √3 Ip
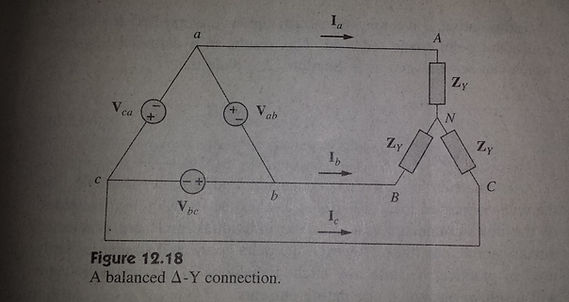
BALANCED DELTA - WYE CONNECTION
A balanced Δ - Y system consists of a balanced Δ-connected feeding a balanced y-connected load.
Ia = Vp/√3 ∠-30 Van =Vp∠-30
Zy √3
Ib = Ia∠-120 Vbn = Vp∠-150
Ic = Ia∠+120 √3
Vcn = Vp∠+90
√3
Similarly we obtain:
Vbc = Vbn−Vcn = √3 Vbn∠30°
Vca = Vcn−Vbn = √3 Vcn∠30°
Learnings from balanced 3-phase systems:
1.The line to line voltages are 3 larger than the line to neutral voltages and they lead the line to neutral voltages by 30°.
2.Geometrically from the voltage triangle (or by using Euler’s formula for the algebraicexpressions) we obtain that
Vab + Vbc + Vca = 0
3.Geometrically from the voltage triangle and rearranging the line to neutral voltages (or byusing Euler’s formula for the algebraic expressions) we obtain that
Van + Vbn + Vcn = 0
4. Three - phase systems are important for three reasons:
First, nearly all electrical power is guaranteed in three - phase. Second, instantaneous power can be constant. Third, more economical than the single - phase.
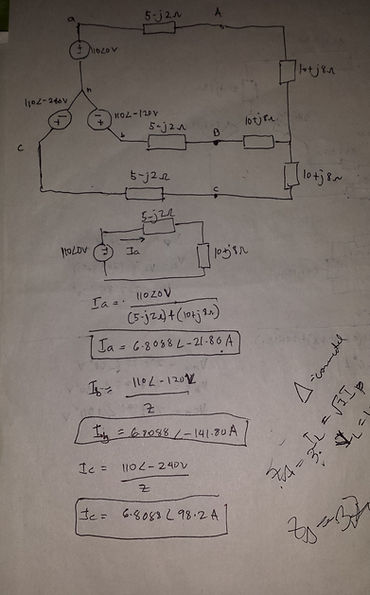

Example:
1.