

MEL TECH
CIRCTRONICS
Thevenin's Theorem
Any combination of batteries and resistances with two terminals can be replaced by a single voltage source V and a single series resistor R. The value of V is the open circuit voltage at the terminals, and the value of R is e divided by the current with the terminals short circuited.

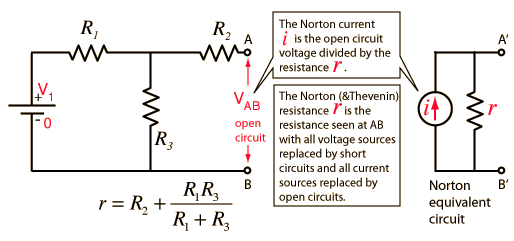
Norton's Theorem
Any collection of batteries and resistances with two terminals is electrically equivalent to an ideal current source I in parallel with a single resistor R. The value of R is the same as that in the Thevenin equivalent and the current I can be found by dividing the open circuit voltage by R.
Maximum Power Transfer (MPT)
The Maximum Power Transfer Theorem is not so much a means of analysis as it is an aid to system design. Simply stated, the maximum amount of power will be dissipated by a load resistance when that load resistance is equal to the Thevenin/Norton resistance of the network supplying the power. If the load resistance is lower or higher than the Thevenin/Norton resistance of the source network, its dissipated power will be less than maximum.
Taking our Thevenin equivalent example circuit, the Maximum Power Transfer Theorem tells us that the load resistance resulting in greatest power dissipation is equal in value to the Thevenin resistance (in this case, 0.8 Ω):
With this value of load resistance, the dissipated power will be 39.2 watts:
